Explaining "Taking features out of superposition with sparse autoencoders"

[Thanks to Logan Riggs and Hoagy for their help writing this post.]

In this post, I’m going to translate the post [Interim research report] Taking features out of superposition with sparse autoencoders by Lee Sharkey, Dan Braun, and beren (henceforth ‘the authors’) into language that makes sense to me, and hopefully you too!

Background

The goal of mechanistic interpretability is “telling simple, human-understandable stories about how individual representations in neural networks relate to each other”. Recall that the internal representation in a neural network is just a vector in R^n (“activation space”). So how do we go from “this is the neural network’s internal state vector” to “here’s the human-understandable story about why the LLM produced the next token”?

One planned strategy revolves around so-called features. It has some assumptions that I’ll label conjectures:

Conjecture 1. There are special vectors in activation space, called features, which (a) correspond to human-understandable concepts and (b) are sufficient to decompose the AI’s internal representation into a simple linear combination of a few features, in a way that enables a clear explanation of the AI’s behavior.

Example 1. Suppose an LLM’s internal state decomposes into 2*[royal feature]+0.5*[male feature]+3*[young feature]. Then we can interpret the LLM as “thinking about” the word “prince”.¹

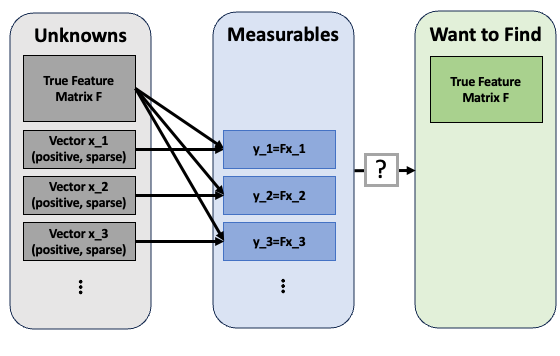
Decomposing a vector (the internal representation) into a linear combination of other vectors (features)? That’s linear algebra! Let’s use this notation:

• n= # of dimensions in activation space.

• h= # of features. We expect h>n.

• F= the n-by-h matrix consisting of the feature vectors.

• Write g(x)=Fx for the linear function from R^h → R^n taking “how much of each feature” to the model’s internal representation.

• We wish to find the inverse of g(x)² to go from the model’s internal representation to how much of each feature it’s using.

Let’s crack open the ol’ linear algebra literature to see what it says about inverting such a linear function… oh, this is impossible because h>n. Oops!

Thus there is a second conjecture:

Conjecture 2. Feature activations are sparse and positive. That is, for any activation vector, it will be a linear combination of just a few features with positive coefficients.

In terms of our inversion problem, we are restricting the domain of g and asking if g-with-a-restricted-domain is invertible. For our new domain, let’s define the set S^h_k, the set of vectors in R^h with positive entries and at most k nonzero entries in the vectors.³

Here’s an example of a setting where this domain restriction makes things possible:

Example 2. S^3_1 consists of just the positive parts of the x, y, and z axes in 3-dimensional space. Under the linear transformation g, each axis maps to ray in R^n, so the image of S^3_1 is the union of 3 rays (one ray per feature). As long as your features in R^n are pairwise linearly independent, g will be injective from S^3_1 into R^n. In particular, even if n=2, you can fit three features into 2-dimensional space.

Example 3. As Example 2, but with S^h_1, which consists of just the positive parts of the h axes in h-dimensional space. The invertibility result can be stated as a nice theorem: as long as no two features in R^n are linearly dependent, g:S^h_1 → R^n will be injective.

A mechanistic interpretability plan then looks like this:

1. Find the vectors corresponding to features (i.e. the matrix F).

2. For each feature, identify the human-understandable concept corresponding to it.

3. Given an activation vector y, find the “feature components” x such that y=Fx, which will be human understandable (e.g. “the LLM said prince because its internal activations were 2*[royal feature]+0.5*[male feature]+3*[young feature]”).

The Goal of Sparse Autoencoders

Suppose conjectures 1 and 2 were true. How would you even find the feature matrix F (step 1 of the mechanistic interpretability plan)⁴? Here’s what the problem looks like:

We measure our data y_1, y_2, y_3…. We know this data was generated by a matrix F and some randomly-chosen positive, sparse vectors x_1, x_2, x_3,… via y_n=Fx_n. The goal of the Sparse Autoencoders post is to reconstruct F.

Example 4. Here’s how this problem might manifest as a game: we agree on h=3, n=3, k=2. I secretly choose h=3 features to be the three standard basis vectors in R^3 (so F=I_3, the 3-by-3 identity matrix). Then, I give you a bunch of points from the XY-, XZ- and YZ-planes (which together form S^3_2). From just that set of points, can you figure out the three features that I blended to make the points?

Dataset Generation

The effort used two dataset: one toy dataset generated as in the previous figure, and one with model activations from a 31-million-parameter language model.

For the toy dataset, they used n=256, h=512. You can think of k as being roughly 5⁵. The feature matrix F consisted of 512 uniformly sampled unit vectors from R^256. The x vectors were produced in a slightly more complicated way so that some features were more common than others, and some pairs of features were relatively (un)likely to activate together. The input dataset was then y_1=Fx_1, …, y_m=Fx_m, where m≈15,000,000.

For the actual language model, they used a small language model with an architecture similar to the GPT models, which I’ll call GPT-Nano. GPT-Nano had 31 million parameters (for context, GPT-1 had 120 million parameters), and it looks like they custom-trained for this task. GPT-Nano has n=256 and h=[humanity doesn’t know, see section Estimating the Number of Features]. The input dataset were the model’s internal activations from layer 2, with m≈15,000,000.

Neural Network Architecture

Okay, so how do we find F? With the eponymous sparse autoencoder! Autoencoders refer to neural networks where the input data is “labelled” by itself, so network learns to squeeze your data into a desired shape in the intermediate layer(s), then reconstructs the data⁶.

Knowing that we measured y=Fx for some fixed matrix F and a random sparse positive matrix x, we can design an architecture and loss function that encourages this kind of reconstruction: our autoencoder will have one hidden layer, which is trying to approximate x by enforcing sparseness and positivity, and the output of the network will be multiplying that (approximation of) x by an (approximation of) F.

The architecture looks like this:

A diagram showing the architecture of the sparse autoencoder. The grey boxes for the True Feature Matrix F and the Specific Feature Coefficients x are not part of the network or the training process, but produce the input data y=Fx.

The input to the network is some y=Fx, and the network tries to reconstruct y after being passed through a hidden layer. The hidden layer is wider than the input layer, but it has an L^1 loss term, which encourages sparse entries. The overall output of the network is z(y)=D*ReLU(Wy+b), where D, W, and b are the learned parameters and ReLU is the usual activation function ReLU(x)=max(x,0). Once the network is trained, the hidden layer vector c=ReLU(Wy+b) acts as a reconstruction of x, and the matrix D acts as our reconstruction of F. There are two components to the loss function: the L^1 norm ||c||_1, which encourages c to be sparse; and the L^2 norm ||z-y||_2, which encourages the network to successfully reconstruct y.

There are two hyperparameters not shown in the diagram:

1. L^1 penalty coefficient α - The overall loss function of the network is a combination of the two orange boxes in the diagram, with coefficient α. That is, training attempts to minimize (overall loss)=(reconstruction loss)+α*(sparsity loss). This coefficient controls the balance between “get an accurate reconstruction” and “the c vectors should be sparse”, with small α favoring the former.

2. Dictionary size J - the dimensionality of the hidden layer, J (labelled as 512 in the diagram).

Scoring Metric

Having the True Feature Matrix F, and producing the “dictionary of features” D, how do we measure if D accurately found the features in F? Simple comparison of matrices is not sufficient, since features might be swapped or rescaled.

Instead, our basic measurement is cosine similarity, which for two vectors u and v is defined as <u, v>/(||u||*||v||), or equivalently the cosine of the angle between u and v. Cosine similarity is 1 if the vectors are “the same” and -1 if they are pointed in exactly opposite directions.

We start by computing the cosine similarity between all the “real features” (columns of F) and the “discovered features” (columns of D). We only care about if some feature in D captures the feature in F, so for each feature f_i we take its maximum cosine similarity across all discovered features d_j. We then average those similarities across the features in F, resulting in the mean max cosine similarity. MMCS is invariant to permutation of the features (due to the mean and the max), and is invariant to positive rescalings (due to using cosine similarity).

For MMCS, larger numbers are better, with a 1 meaning a perfect reconstruction, where D contains the exact true features in F.

Outcomes on Toy Dataset

The headline result is that this works at all - you are able to reconstruct the feature matrix F quite well, using just this surprisingly simple architecture!

Then we get to hyperparameter questions: what values of the L1 penalty coefficient α and the dictionary size J worked well?

On their toy dataset, they find that a range of values of α work, “from around 0.03 to around 0.3”:

Figure 1 from the post, showing how a range of L1 penalty coefficients α all produce a good reconstruction of F.

What about the dictionary size J? They find that you need a dictionary at least as large as the number of features (J≥h), as you’d expect, but that there’s a wide plateau up through J≈8h:

Figure 2 from the post, showing how a range of dictionary sizes produce a good reconstruction of F.

Estimating the Number of Features

Moving from the toy dataset to the LLM dataset, we have to make a choice of J, the dictionary size. We know from the toy dataset it’s best if J is slightly larger than h, the number of features in the LLM, but we don’t know that number either!

The authors suggest three techniques for finding the right J value:

1. Increase J until you get dead neurons in the hidden layer. A dead neuron is one that always has value 0, and while J<h each neuron is too “valuable” to leave dead. But once J>h, the autoencoder may not “need” all the hidden layer neurons, so some of them will be dead, which we can measure even if we don’t know the ground truth h.

2. Loss stickiness. I’ll be honest, this approach is less clear to me (and the authors concede “Using this plot to determine the right dictionary size is harder”). But I think the idea is that you sweep over L1 coefficients at different J values. When the J value is too small, the L1 loss decreases uniformly, but if J is sufficiently large, there is a range of L1 coefficients that all give similar results. So if you see that basin, you know you’re in the right J range.

3. Mean max cosine similarity between a dictionary and those larger than it. The authors think they can compare two learned dictionaries to each other as a way of estimating when J is correct. The first step in their reasoning is thinking about what dictionary features are learned when J is the right size, too large, or too small:

   1. J right size - D learns the canonical features in F.

   2. J too large - D learns the canonical features in F, and also “extraneous features”, either dead neurons or multiple copies of canonical features.

   3. J too small - D learns the most common canonical features, or combinations of features. (For instance, if f_1 and f_2 are correlated features that usually appear together, D might learn f_1+f_2.)

   Now consider what happens when you train two dictionaries of these two sizes, and compute the Mean Max Cosine Similarity between the smaller and larger:

   

   Theorized Mean Max Cosine Similarity (MMCS) between dictionaries of varying sizes. Note that right-sized dictionaries can be identified by their high MMCS (green cells). Italicized cells were not directly addressed in the research report, so I filled them in with my own speculation.

   Thus one can identify right-sized dictionaries as those which have high MMCS with other dictionaries of similar size and larger size, but not smaller size. The authors claim this technique works⁷.

Applying these techniques to GPT-Nano, they get these estimates for the number of features:

1. Dead Neurons: 100K features

2. Loss Stickiness: No confident estimate, but major loss improvement at 1K features, and the flat region appears around 32K features.

3. Mean max cosine similarity between a dictionary and those larger than it: This technique doesn’t seem to hold up, perhaps due to noise. But in the follow-up small update post, they suspect that the issue is due to “severely undertrained sparse autoencoders”.

Conclusion

The technique works very well on toy data, but less well on GPT-Nano. The rough estimate of the number of features is alarming, that there may be 100K features hiding in 256 dimensions, and if that ratio of features:dimensions persists, it may be hard to scale to a full-size LLM. It’s unclear why the technique works less well on the real LLM, but some possibilities are:

• The conjectures are wrong about how LLMs represent their internals.

• The autoencoders were too small or undertrained.

• The toy data failed to capture something in the real data, such as the number of features, noise, or some kind of correlations between the features.

1. This is my own idealized example, the reality is undoubtably more complicated. In these followup slides, they extract some features and found these descriptions of them:

• 60: Greek letters

• 62: Full stop after “blogger” in url

• 73: Some kind of quantifiers/modifier-like thing?

• 240: August and march (but also "section")

• 324: Commas after numbers

2. Technically, we only care about finding a left-inverse, so it’s okay if g fails to be surjective, as long as its injective.

3. It may be somewhat misleading to fix a k. In reality it might be more like 90% of internal representations come from S^n_k, 95% come from S^n_{k+1}, 99% from S^n_{k+2}, etc.

4. This effort was primarily aimed at solving step 1 of the interpretability plan, but incidentally makes progress on step 3. The research team has done some followup work trying to make progress on step 2 by hand. Compare with step 1 of this blog post, where OpenAI tries to have GPT-4 do our step 2 on GPT-2 neurons.

5. On average, activations were a combination of 5 features. The actual number of features present in each activation would follow a binomial distribution of 512 trials, with each trial having probability of success 5/512.

6. A classic use for autoencoders is compression/dimensionality reduction of your data. For instance you might make a neural network with a 100-dimensional input/output channel and a single 20-dimensional hidden layer, which would force your network to find the “most important” 20 dimensions.

7. I think I disagree with the author’s read of their data here: in their Figure 10 (below), it seems that MMCS is very high across a range of (α, J) pairs, including some where J<h. In fact, in their diagram it looks like the highest MMCS is attained at J=.5h, α=0.18, a dictionary that is too small! I would conjecture that what went wrong is that the dictionary does not learn combinations of features, and instead learns canonical features in descending order of frequency. Thus a small dictionary would have high MMCS with a right-size dictionary, since they both consist of the canonical features.

Figure 10 from the post. Original caption: Mean Max Cosine Similarity between a dictionary and dictionaries larger than it, for different L1 penalty coefficients and dictionary sizes. For the dictionary sizes which have multiple larger dictionaries, we take the mean of the set of MMCS values.