How does GPT-3 spend its 175B parameters?
Or: This question consumed a week of my life
[Target audience: Me from a week ago, and people who have some understanding of ML but want to understand transformers better on a technical level.]
[AI Safety relevance rating: NI]
Free advice for people learning new skills: ask yourself random questions. In answering them, you’ll strengthen your understanding and find out what you really understand and what’s actually useful. And some day, if you ask yourself a question that no one has asked before, that’s a publication waiting to happen!
So as I was reading up on transformers, I got fixated on this question: where are the 175 billion parameters in the architecture? Not in the literal sense (the parameters are in the computer), but how are they “spent” between various parts of the architecture - the attention heads vs feed-forward networks, for instance. And how can one calculate the number of parameters from the architecture’s “size hyperparameters” like dimensionality and number of layers?
The goal of this post is to answer those questions, and make sense of this nice table from the GPT-3 paper, deriving the n_params column from the other columns.

Primary Sources
Lots of resources about transformers conjure information from thin air, and I want to avoid that, so I’m showing all my work here. These are the relevant parts of the sources1 we'll draw from:

Three more details we’ll use, all from Section 2.1 of the GPT-3 paper:
The vocabulary size is [n_vocab=]50257 tokens (via a reference to Section 2.3 of the GPT-2 paper)
The feed-forward networks are all a single layer which is “four times the size of the bottleneck layer”, so d_ff = 4*d_model
“All models use a context window of n_ctx = 2048 tokens.”
Variable abbreviations
I’ll use shorthand for the model size variables to increase legibility:
n_layers = x
d_model = y
n_heads = z
d_head = w
n_vocab = v
n_ctx = u
Where are the Parameters?
From Exhibit A, we can see that the original 1-hot encoding of tokens U is first converted to the initial “residual stream” h_0, then passed through transformer blocks (shown in Exhibits B-D), with n_layers blocks total2. We'll break down parameter usage by stage:
Word Embedding Parameters
W_e is the word embedding matrix.
Converts the shape (n_ctx, n_vocab) matrix U into a (n_ctx, d_model) matrix, so W_e has size (n_vocab, d_model), resulting in vy = n_vocab*d_model parameters.
Position Embedding Parameters
W_p is the position embedding matrix. Unlike the original transformer paper, GPT learns its position embeddings.
W_p is the same size as the residual stream, (n_ctx, d_model), resulting in uy = n_ctx*d_model parameters
Transformer Parameters - Attention
The attention sublayer of the transformer is one half of the basic transformer block (Exhibit B). As shown in Exhibit C, each attention head in each layer is parameterized by 3 matrices, W_i^Q, W_i^K, W_i^V, with one additional matrix W^O3 per layer which combines the attention heads.
What Exhibit C calls d_k and d_v are both what GPT calls d_head, so W_i^Q, W_i^K, and W_i^V are all size (d_model, d_head). Thus each attention head contributes 3*d_model*d_head parameters.
What Exhibit C calls h is what GPT calls n_heads, so W^O is size (n_heads*d_head, d_model) and therefore contributes n_heads*d_head*d_model parameters.
Total parameters per layer: For a single layer, there are n_heads attention heads, the W_i^Q, W_i^K, and W_i^V matrices contribute (3*d_model*d_head)*n_heads parameters, plus an additional n_heads*d_head*d_model parameters from W^O, for a total of 4*d_model*d_head*n_heads
Total parameters: 4xyzw = 4*d_model*d_head*n_heads*n_layers
Transformer Parameters - FFN
The “feed-forward network” (FFN) is the other half of the basic transformer block (Exhibit B). Exhibit D shows that it consists of a linear transform parameterized by W_1 and b_1, an activation function, and then another linear transform parameterized by W_2 and b_2, as one might see in an MLP with one hidden layer4. Note the remark in Exhibit D: “the linear transformations are the same across different positions, [but] use different parameters from layer to layer”, so we have one set of parameters (W_1, W_2, b_1, b_2) per layer.
The matrices W_1 and W_2 are size (d_model, d_ff) and (d_ff, d_model) respectively. Since d_ff=4*d_model, each one contributes 4*d_model^2 parameters.
The bias terms b_1 and b_2 are size d_ff=4*d_model and d_model respectively, so they contribute 5*d_model parameters.
Total parameters per layer: 8*d_model^2+5*d_model parameters
Total parameters: 8 xy^2 + 5xy = 8*d_model^2*n_layers+5*d_model*n_layers parameters
Other Components
The other components of the transformer architecture (such as the layer-norm in the “add and norm” block in Exhibit B) doesn’t use any parameters.
In total there are vy + uy + 4xyzw + 8xy^2 + 5xy = (n_vocab*d_model) + (n_ctx*d_model) + (4*d_model*d_head*n_heads*n_layers) + (8*d_model^2*n_layers) + (5*d_model * n_layers) parameters.
Is this correct?
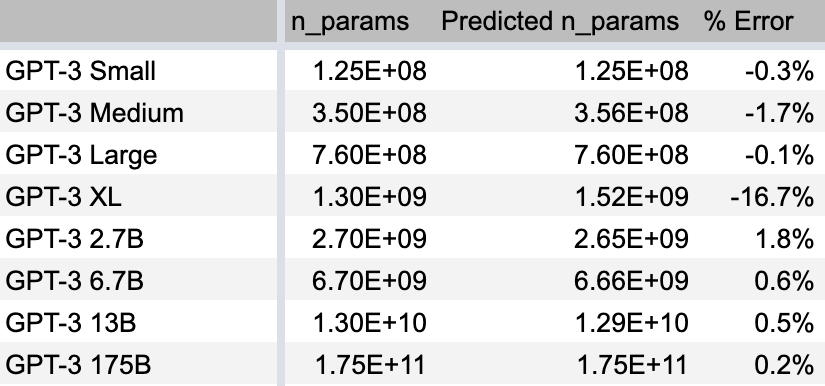
Here’s a spreadsheet computing these values. Here’s how we did:
With one exception, that’s great! Our errors are ~1%! This takes me back to my college physics labs where the theory matches the “experiment” amazingly well. In the other tabs of the spreadsheet you can see we also do well at predicting the model sizes of the GPT-2 variants.
The one exception is GPT-3 XL, where we’re off significantly. We’ll discuss this more in the final section.
Analysis
Let’s look at some implications.
How many parameters are spent on each part of the architecture?
Now we can answer “how many parameters are used in the attention vs FFN parts of the architecture”":
We can see that:
Position embedding always take very few parameters.
Word embedding takes about 30% of the parameters for the smallest model, but a proportionally smaller amount as the model gets larger, ultimately <1% of parameters for the full-size GPT-3.
The remaining parameters are split 2:1 between the feed-forward network and the attention heads, except in GPT-3 XL, where there’s a 4:3 split. However, there’s nothing sacred about this 2:1 split. It’s a function of the ratio y:wz (which is 1:1 in all models except XL) and the FFN architecture (1 hidden layer with d_ff=4*d_model), both conventions inherited from the original transformer paper.
How does model size depend on size hyperparameters?
For large models, the only terms that contribute significantly to the parameter count are the attention weights and non-bias FFN weights, which contribute 4xyzw and 8xy^2 parameters, respectively (recall that x=n_layers, y=d_model, z=n_heads, and w=d_head). For almost all GPT-3 sizes, y=zw, a convention adopted from the original transformer paper5, in which case the parameter count is O(xy^2). So parameter cost increases directly with the number of layers, but with the square of the internal dimensionality.
Guessing the size hyperparameters of GPT-4 from n_params
Right now a hot trend on twitter is to hold your breath until you see a biblically accurate angel, count its eyes, and claim that GPT-4 will have that many parameters6.
Here at AIZI, we would never engage in such baseless speculation. Instead, let’s take that baseless speculation as factual and engage in a different baseless speculation: If we assume GPT-4 will have 100 trillion parameters and the same architecture as GPT-3, we can use numerical methods7 to find potential size hyperparameters. With 2^k layers and model size 2^m, you reach 100 trillion parameters when k+2m = 43. With k=9 and m=17, you have 512 layers and 131072-dimensional inner states, which has the benefit of sexy headline sizes increases over GPT-3: 500x parameters! 5x layers! 10x dimensionality!
Analysis of Transformers must include the FFNs
I love this work, where they analyze transformers that don’t have feed-forward networks, using them as the simplest example to build from. But knowing that two-thirds of GPT-3’s parameters are in the FFN sublayers means this approach alone is missing a lot of the picture. (And the amount its missing could be much more than 2/3rds of the picture: the FFN and attention sublayers are “mixing” information in different ways, so allowing both likely generates far more complexity than either one individually).
Open Questions
This project has given me a much better grasp of what’s going on in transformers, but there are questions I still haven’t answered yet:
Why was my prediction wrong about GPT-3 XL? You can fix the prediction by replacing the 4xyzw term with 4xy^2, which you can see on columns AA-AB of the spreadsheet, which works because y=zw for all models except XL, where 1.5y=zw. But I think the 4xyzw term should be correct, in which case the GPT-3 table must have a typo in the number of parameters or the size hyperparameters. Am I wrong or is that a typo in the GPT-3 paper?
Why does GPT-3 use the same matrix for word embedding and final predictions? I would expect this to constrain the model, and the only potential upsides I can see are saving parameters (lol) and preserving interpretability (lmao)8. Other resources like A Mathematical Framework for Transformer Circuits use different embedding/unembedding matrices - their W_E and W_U. Perhaps this is not necessary for GPT-3 since the final feed-forward network can perform an appropriate linear transformation, and in A Mathematical Framework they are looking at transformers without FFNs. But some properties (e.g. words being linear combinations of other words) cannot be changed by such a linear transformation, so having an entire new unembedding matrix could still add value.
The GPT-3 paper says “we use alternating dense and locally banded sparse attention patterns in the layers of the transformer”, citing this paper, and this sounds like it should affect the number of parameters! But our calculations never took this into account, and seem to be correct. What do they mean by sparse transformers? What do they contribute? Why am I able to compute the correct number of parameters by ignoring their “alternating dense and locally banded sparse attention patterns”?
GPT is called a “decoder only” architecture. Would “encoder only” be equally correct? From my reading of the original transformer paper, encoder and decoder blocks are the same except that decoder blocks attend to the final encoder block. Since GPT never attends to any previous block, if anything I feel like the correct term is “encoder only”.
Why not increase the context length and vocabulary size? The parameter costs of a larger context window and vocabulary size would be trivial. I could imagine that the vocabulary is already “good enough” and doesn’t need improving, but why not increase context length? Could this be the related to the “compute costs” I’ve heard rumors of?
If you know the answer to any of these questions, please leave an answer in the comments!
Links to works cited, in order of appearance:
Improving Language Understanding by Generative Pre-Training (“the GPT-1 paper” and yes I know GPT-1 is actually just GPT but I think its clearer to refer to it as GPT-1 in this context)
Attention Is All You Need (“the original transformer paper”)
Language Models are Few-Shot Learners (“the GPT-3 paper”)
Language Models are Unsupervised Multitask Learners (“the GPT-2 paper”)
I also like these resources for learning about transformers:
A Mathematical Framework for Transformer Circuits - An analysis of shallow transformers, highly recommended for including thorough detail missing in the papers.
The Illustrated Transformer - An info post with lots of pictures.
Building a ML Transformer in a Spreadsheet - A video an accompanying spreadsheet that implements a simple transformer (with hand-coded weights).
In the final P(u) calculation the word embedding matrix W_e is reused from step 1, so it doesn’t add more parameters. Although it’s possible to build a transformer with a different unembedding matrix, the parameter calculations come out correctly if you reuse these parameters.
One could equivalently break W^O into n_heads matrices W_i^O, which is far more intuitive IMO, but I’ll try to keep the paper’s notation.
The original transformer used RELU as its activation function, but the GPT-1 paper uses GELU, which I think is carried forward into GPT-3. Regardless, the activation function does not contribute any parameters.
The original transformer explains that splitting attention between heads makes “the total computational cost… similar to that of single-head attention with full dimensionality.” Also, that’s enough dimensionality that the model can read the full dimensionality of the previous layer. So if, for a fixed model size y, computational and parameter costs are ~constant along the curve y=zw, what are you trading off by choosing larger or small z and w? The GPT-3 models choose different values for the w:z ratio, always with w>z, but otherwise varying the ratio. I also wonder if there’s reason to experiment with zw>y, to see if that leads to better performance (and OpenAI seems to have tried that, in GPT-3 XL, zw/y=1.5).
I’m not going to link to all the ridiculous proclamations on twitter, but a popular guess is 100 trillion parameters. The strongest source I can find for that number is this interview with Andrew Feldman, but Andrew Feldman a) doesn’t work at OpenAI, b) was speaking in 2021 aka an eternity ago, and c) was giving a rough estimate.
guess and check
For those who are not terminally online, this translates to “those ships have sailed, this would increase parameters from 175B to 175.6B and decrease interpretability from 0 to 0”.



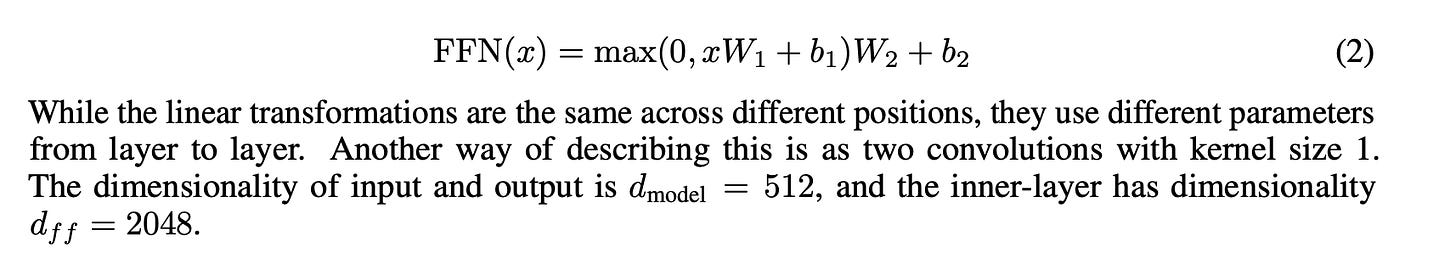

I looked into Question 4 as well and when considering encoder-only or decoder-only transformers, neither uses the extra "Encoder-Decoder Attention" Layer, so they're almost identical in their structure. The only difference is that the encoder uses normal self-attention, whereas the decoder uses masked self-attention. However, from my understanding, this is only relevant at training time, so the decoder does not "cheat" by attending to future (known) tokens. But since at inference time, the decoder by definition does not have any future tokens to look at, I really think the difference is only in terms of training (and maybe also when "ingesting" the prompt). This would explain why "encoder-only" models such as BERT are seen as better at classification (you look at the whole sequence) whereas "decoder-only" models such as GPT are better at text generation.
On Open Question 2., this paper possibly explains why: https://arxiv.org/pdf/1608.05859.pdf