No Really, Attention is ALL You Need
Attention can do feedforward networks
[AI Safety Relevance Rating: AI]
[Epistemic status: Mathematically proven, and I have running code that implements it.]
[Edit/Update: I describe a more efficient implementation here.]
Overview: A transformer consists of two alternating sublayers: attention heads and feedforward networks (FFNs, also called MLPs). In this post I’ll show how you can implement the latter using the former, and how you can convert an existing transformer with FFNs into an attention-only transformer.
My hope is that such a conversion technique can augment mechanistic interpretability tools such as the ones described in A Mathematical Framework for Transformer Circuits, by reducing the task of interpretability from “interpret attention and FFNs” to just “interpret attention”. That publication specifically points out that “more complete understanding [of Transformers] will require progress on MLP layers”, which I hope this technique can supply.
Limitations:
Attention heads are able to naturally produce two activation functions, SiLU and ReLU, but I haven’t found an easy way to produce GeLU, which is what GPT uses.
SiLU is qualitatively similar to GeLU, especially after rescaling. Of course one can approximate other activation functions by adding more layers.
Converting to attention-only introduces small error terms in the calculations, but such terms can be made arbitrarily small (potentially small enough that a machine rounds it to 0).
Attention-only transformers are likely to be worse for capabilities than normal transformers. Since my goal is safety rather than capabilities, this is a feature and not a bug for me.
Appealing to authority, the people currently making transformers optimized for capabilities use FFNs in addition to attention heads. If attention-only transformers were better for capabilities, they’d presumably already be in use.
Implementing an FFN via attention this way is computationally slower/more expensive than a normal FFN.
Converting to an attention-only transformer increases d_model by ~5x. Most of the additional dimensions are used to store what was previously the hidden layer of the FFN, and a few more are used for 1-hot positional encoding.
Converting to an attention-only transformer replaces each each FFN sublayer with 3 attention layers, so a whole layer goes from 1 attention+1 FFN to 4 attention.
Some matrices used by the new attention heads are higher rank than the normal head dimensions allow. This would require a special case in the code, slow down computation.
The structures used for attention-only transformers are probably not stable under training with any form of regularization.
This result may already be known, but is new to me (and therefore might be new to some of you).
Notation
Fix a transformer T (such as GPT-3) which uses attention and feedforward networks. Write D=d_model for the internal dimension of the model, N=n_ctx for the number of vectors in the context, and X for the “residual stream”, the N-by-D matrix storing the internal state of the model during a forward pass.
We will assume that the feedforward networks in T consists of an MLP with one hidden layer of width d_ff=4*d_model, using an activation function α(x)=SiLU(x)=xσ(x)1. To simplify notation, we will assume that bias terms are built into the weight matrices W_1 and W_2, which are respectively of sizes D-by-4D and 4D-by-D, so that the output of the feedforward network is α(X*W_1)*W_2, where α is applied to the matrix entry-wise.
We’ll follow this notation for attention heads, so that an attention head is characterized by its query-key matrix Q=W_QK and its output-value matrix V=W_OV, each of size D-by-D2. To simplify notation, we will assume that the “/sqrt(d_k)” step of attention has been folded into the Q matrix. Then the output of the attention head is softmax[XQ(X^T)]XV, where the softmax operation is applied row-wise.
We assume that both the feedforward network and attention heads make use of skip connections, so that their output is added to the original residual stream. However, we ignore layer normalization.
Throughout, we will rely on a large number Ω whose purpose is to dwarf other numbers in the softmax operation of an attention head. In particular, we assume Ω has two properties:
softmax(Ω, 0, 0, …, 0)=(1, 0, 0, …, 0), to within an acceptable error, when there are up to N 0s. That is, with an error tolerance of ε>0, one needs exp(Ω)>N/ε.
Ω > |x| for each x that appears in an attention entry in the normal operation of T.
In my code, Ω=1000 is sufficient for a tolerance of ε=10^-10.
Construction Overview
We will convert the attention-and-feedforward model T into an attention-only model T’ by augmenting the residual stream, replacing the feedforward sublayers with attention sublayers, and tweaking the original attention heads to maintain their original behavior on the augmented residual stream.
We augment the residual stream of the model by:
N’ = N+1. The new context vector will act as a “bias context vector” which we use to implement the entrywise SiLU function.
D’=D+4D+(N+1). The 4D additional dimensions will be used to store the intermediate calculations of the FFN network. Then N+1=N’ additional dimensions act as 1-hot positional encodings.
In T, each layer consists of two sublayers:
Multi-headed attention.
Feedforward network.
In T’, these are replaced by:
Multi-headed attention. This acts identically to the original transformer, though the Q and V matrices are slightly tweaked to avoid issues arising from introducing the “bias context” vector.
Linear transformation via attention heads. This transformation emulates X*W_1 by reading from the D-width residual stream and writing to the 4D-width residual stream corresponding to the hidden layer. The Q matrix makes each vector only attends to itself, and the V matrix contains a copy of W_1.
Entry-wise SiLU to hidden layers via attention heads. Using one attention head per dimension, we apply the activation function to the “hidden dimensions” computed in the previous step, resulting in α(X*W_1). The Q matrix makes each vector attend only to itself and the final “bias context” vector, split in proportion to σ(x). The V matrix makes a vector write the negative of its entry and the bias context vector write 0, resulting in an entrywise SiLU.
Linear transformation via attention heads. This step emulates multiplying by W_2 and adding it back to the D-width residual stream. This step also zeroes out the 4D-width part of the residual stream corresponding to the hidden layer, readying them to be written to by the next layer. The Q matrix makes each vector only attends to itself, and the V matrix contains a copy of W_2.
The following sections will discuss these steps in the order (3), (2+4), (1), which is descending order of novelty to me.
Entry-wise SiLU via attention heads
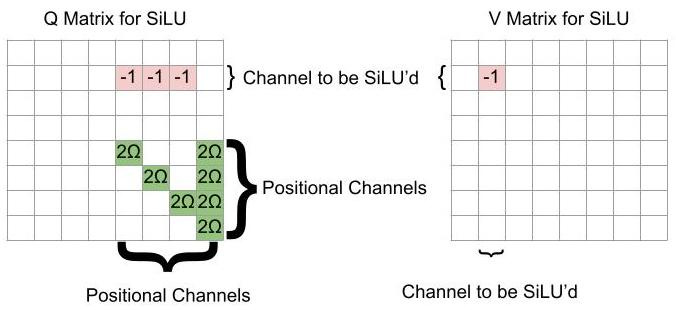
One can apply SiLU to the residual stream with one attention head per dimension being SiLU’d. One uses the following Q and V matrices:
With this Q matrix, the jth row of XQX^T will be of the form [-x_jk, -x_jk, …, -x_jk, 2Ω-x_jk, -x_jk,…., -x_jk, 2Ω], where k is the dimension being SiLU’d, and the 2Ωs are in the jth entry and the final entry. Then, after applying the softmax to this row, the row becomes [0, 0, …, 0, 1-σ(x_jk), 0,…, 0, σ(-x_jk)] (to within error). That is, every vector is attended by only itself and the bias vector.
By our choice of V, the influence of a vector is the negative of its entry in the kth position. Thus the jkth entry of softmax[XQ(X^T)]XV is -x_jk(1-σ(x_jk)), so after adding to the residual stream, one gets that the jkth entry of X+softmax[XQ(X^T)]XV is x_jkσ(x_jk)=SiLU(x_jk), as desired.
Vector-Wise Linear Transformations via Attention Heads
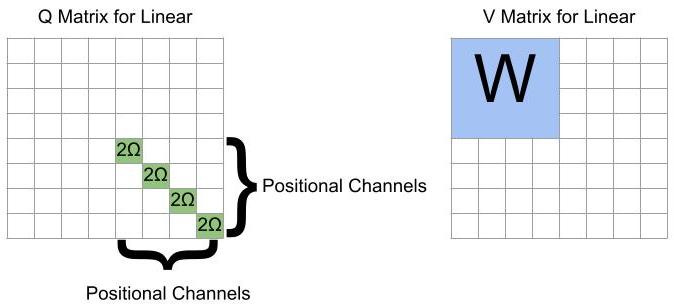
By putting such large weights in the self-positional-encoding matrices, a vector attends entirely to itself. Thus the output of the attention head is entirely the result of the V matrix, which can contain the arbitrary linear transformation of the feedforward network. Additional comments:
If one is trying to write from the “normal dimensions” to the “hidden dimensions”, or vice-versa, the W matrix must be placed as a block off the diagonal.
If the weight matrix W is too high-rank, it can be split over multiple attention heads with equal Q matrices.
One can be cute and use the 1s in the position encoding dimensions for the bias terms.
We also use this step to “clear the memory” by zeroing out the 4D additional dimensions used to save the hidden layer of the FFN.
Tweaking the Original Attention Heads to Preserve Their Behavior
The addition of the new vector used for the activation function could potentially change the attention patterns of the preexisting attention heads, which would change the behavior of the network. However, we can slightly tweak the attention matrices in a normal attention head to prevent this issue:
By augmenting the attention matrix in this way, the bias vector strongly avoids attending to the non-bias vectors, and strongly attends to itself (preventing non-bias vectors from attending to the bias vector).
Demonstration Code
I’ve put Python code implementing this technique on github. Each of the three components (SiLU, linear transformations, normal attention) are implemented both directly and with attention heads. They are tested on random matrices with N=20 and D=30, and the largest error entries in each matrix are on the order of 10^(-14). I have not tested how such errors propagate through multiple layers.
Conclusion
Attention heads can implement the feedforward network components of a transformer, up to small errors.
It is possible to convert an existing transformer to such an attention-only network as long as the original network uses SiLU or ReLU as its activation function. This makes the transformer larger and slower, but not astronomically so.
Such conversion could assist in mechanistic interpretability efforts which are able to operate on attention heads but not FFNs, such as this work.
Several hurdles would need to be overcome before this technique could lead to capabilities gains.
There is significant wasted computation in the attention heads emulating the FFN network.
Many of the attention patterns we use are higher rank than are allowable by the fact that Q is learned as a low-rank matrix factorization (Q=W_Q*W_K^T). In GPT-3 the largest learnable rank is d_head=128, but both the SiLU heads and the linear transformation heads use attention patterns of rank n_ctx=2048.
L2 regularization during training would likely make the attention matrices used in SiLU heads and linear heads unstable by reducing the Ω entries.
Dropout regularization during training would also be disruptive, since the attention patterns rely on strong signals from specific entries, with no redundancy.
One can also approximate ReLU with this technique, since SiLU(kx)/k → ReLU(x) as k→infinity. AIAYN uses ReLU, but GPT-3 uses GeLU.
For implementation purposes, these matrices are usually learned as low-rank factorizations, with W_QK=W_Q*(W_K^T) and a similar expression for W_OV. However, it’s easier to construct the desired properties if we treat them in their full form. We will ignore rank restrictions except in the concluding comments.