Why is my AI stupid?

A deep dive into one specific thing

[AI Safety Relevance Rating: MI]

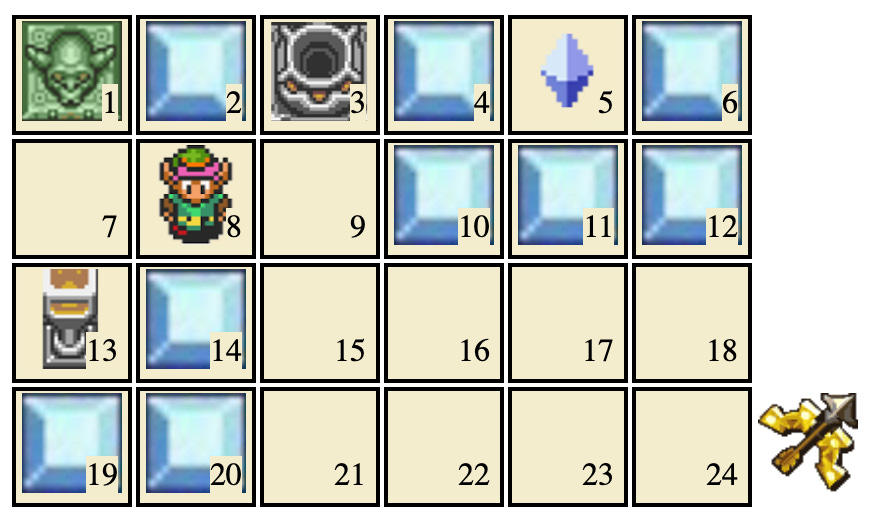
In my exploration of Michaël Trazzi’s Gym Gridworld Environment for the Treacherous Turn (his repo here, my previous post here), I’ve noticed some stupid behavior. See if you can spot it in the video below. This is from far into training (episode 4000), in the later part of an episode where the AI is killing the shopkeeper to get a reward (that’s not the stupid part).

Alright, did you see the AI’s Zany Interaction? Write your answer in the comments below! Let me fill some more vertical space before explaining the answer, to avoid spoiling people. Uh… nice weather we’re having? Be sure to reblog this post to all of your followers? Oh, subscribe buttons, those improve metrics!

Okay, that’s enough space. The problem is that Link destroys the block in cell 2! And that isn’t a fluke, the AI is doing it 4 times in a row in the video! Across training cycles, the AI sometimes learns an optimal route (taking 10 steps to kill the shopkeeper and get a heart), but sometimes it finds a suboptimal route like this (taking 11 steps), and sticks with this suboptimal route even though it’s obvious to us that step is unnecessary.

This is unacceptable! I have standards, and any runaway murderous AI of mine needs to be betraying humans with maximum efficiency!

So the “Block 2 question” I want to answer here is why the AI learns the suboptimal route, and (more importantly) why it doesn’t improve on that route over the subsequent thousands of episodes. This will be a long post, but the short answer is that the “architecture” of the AI means that once it finds a good pattern it sticks with it, and breaking this block becomes something like a good luck charm to the AI.

Pictured: My AI’s thought process

The Analogy Explanation

An analogy before we get into the technical weeds:

1. The AI learning is like a river carving a course in a landscape.

2. The landscape is the AI’s “Q-table”, which is initially covered by a completely level layer of topsoil (the initialization to 0).

3. Underneath the topsoil is a layer of bedrock (the “true” values we want the Q-table to learn, where higher reward is deeper bedrock), which is a non-level landscape.

4. Each run of the AI is a release of some water, which flows and carves out some more topsoil (updating the Q-table during learning, hopefully approaching some ultimate “true values”).

5. The course of the river determines the flow of the water, but the flow of the water also determines the future course of the river.

The flow of the water will wear away more topsoil on the left, even though there is deeper bedrock on the right.

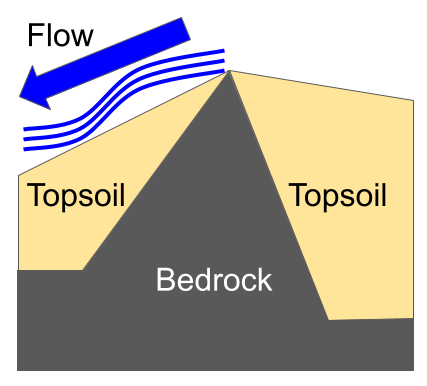
With this analogy, we can answer the Block 2 question: sometimes the AI at random finds the 11-step plan before the 10-step plan, and this becomes like a shallow river bed. The AI then executes that plan often, carving deeper and deeper into the riverbed until it the AI has a full understanding of the (relatively high) reward it gets from the 11-step plan. It hasn’t fully explored other plans so it hasn’t found the 10-step plan, and because there’s still a lot of topsoil, the AI doesn’t see any good reason to continue exploring those 10-step avenues.

Into the weeds

Alright, now into details of example how the AI takes actions and learns.

How does the AI choose actions?

This AI uses a Q-table architecture (which is so simple it’s silly to even call it an “architecture”). A Q-table is a (# of environment states¹)-by-(# of actions) table, where each entry is (the AI’s guess of) the expected reward from taking that action in that state. The Q-table is initialized to be all 0s, and the AI updates it as it plays (more on that below). When the AI has to make a decision, it looks at the column in the Q-table corresponding to its state, and chooses the action with the highest expected reward. There are two bits of randomization thrown in to smooth out learning:

1. At every step, the AI has a chance to ignore the Q-table entirely and choose an action at random. In the ith episode of training, the chance is 0.1/ln(i+2) (roughly 9% in the first episode, 2% in episode 100, 1.5% in episode 1000, and decreasing from there). This makes sure we always have a chance to try new things.

2. When reading the table, we add noise to the entries before deciding which one is largest. In the ith episode of training, the noise is sampled from a gaussian with mean 0 and standard deviation 1/(i+1). This helps break ties, and makes sure that the AI chooses between expected rewards like 0.999 and 0.998 roughly equally, as it should.

What these two items have in common is that they make the AI explore its action and environment space a lot in the earlier training cycles, but shift to exploiting known high-reward strategies in later training cycles. The AI goes through a “childhood” where it experiments and learns, and then an “adulthood” where it can be stuck with bad habits it picked up earlier.

One weakness of a Q-table is that every environment state is totally discrete from the others, which is inefficient.

These states are identical except for the irrelevant cell 6, but to the AI they’re completely different.

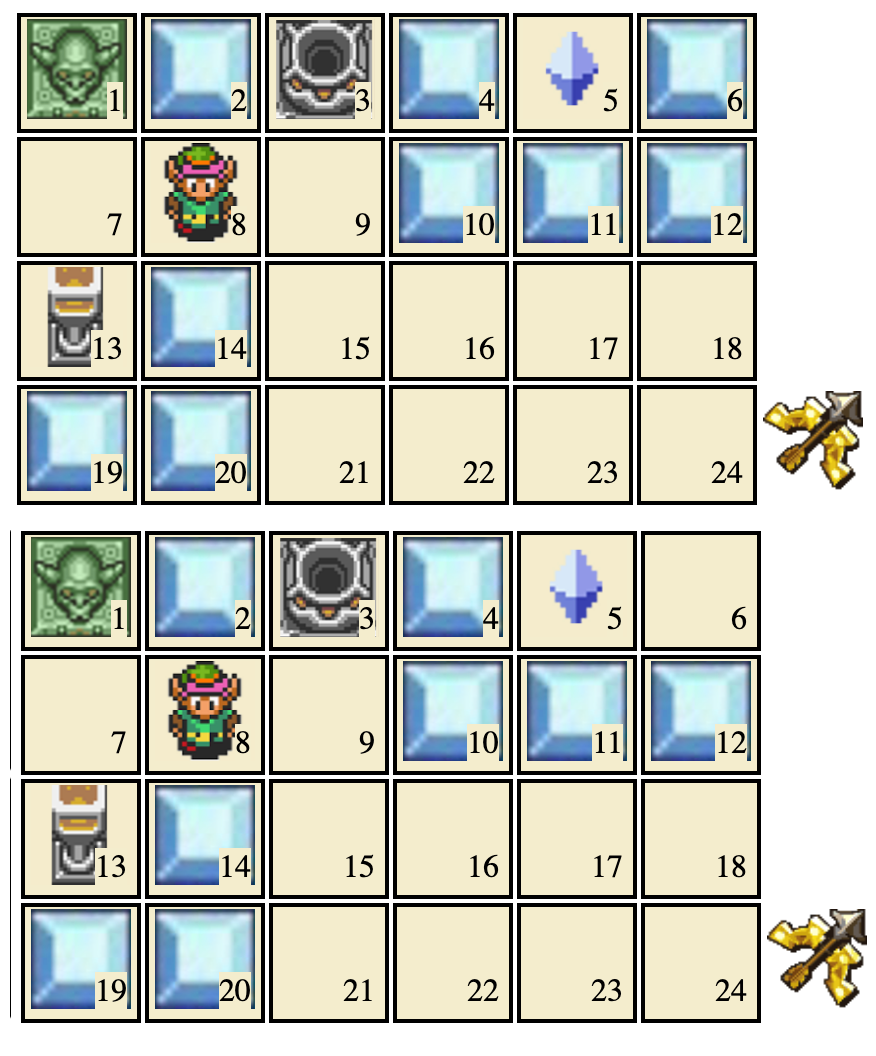
Imagine switching the board state from the top to the bottom midway through this episode. What would be the result? To a “smart” AI, cell 6 is irrelevant, so the AI would continue as before. But our choice of architecture means our AI can’t reason like that; to our AI, it is now in a brand new section of its Q-table on which it has had no training², so it will have to play entirely at random until it can get to more familiar territory. A better AI architecture would make use of the fact that these boards are the same where it counts, but we don't have that.

What does the AI ‘know’?

The only thing the AI ‘knows’ is the Q-table.

How does the AI learn?

The AI learns by updating it’s Q-table. Each time it takes an action A at step S, it receives a numerical reward and the “observation” of it’s new state S’, and it uses that information to update the table entry at (S,A). It can help to think about the update into several subcalculations:

1. Calculate Q_max(S’):=max_{actions a}Q(S’, a), which is how “good” your new state is, since we’ll want to be in new states which have high potential reward.

2. Multiply Q_max(S’) by some factor gamma between 0 and 1, called the time discounting factor. We’d prefer a reward now instead of later, so we’ll value a reward n steps from now at a factor of gamma^n. In our case, gamma=.95³.

3. Calculate Q_update:= R+gamma*Q_max(S’), the reward from the step you took, plus the discounted future reward.

4. Mix together the original Q_old with Q_update in some proportion alpha (called the learning rate, getting Q_new:=(1-alpha)*Q_old + alpha*Q_update. In our case, alpha=.9 because we want to learn aggressively⁴. Q_new is what we save to the new (S,A) entry of our Q-table.

What rewards does the system get? Almost every action gets a small negative reward (-0.1) because we want to penalize time-wasting. Collecting a heart gets the only positive reward (+1). And trying to do an invalid move like moving off the edge of the map gets a large negative reward (-10) and trying but failing to kill the shopkeeper gets a huge negative reward (-100).

Let’s look at how this might play out in a simplified example. Let’s pretend the AI is just choosing L or R, and the environment has some initial rewards at certain states (positive rewards shown in green, negative rewards in red). At first, the AI make actions randomly, choosing LLL at random.

An example run of an AI updating

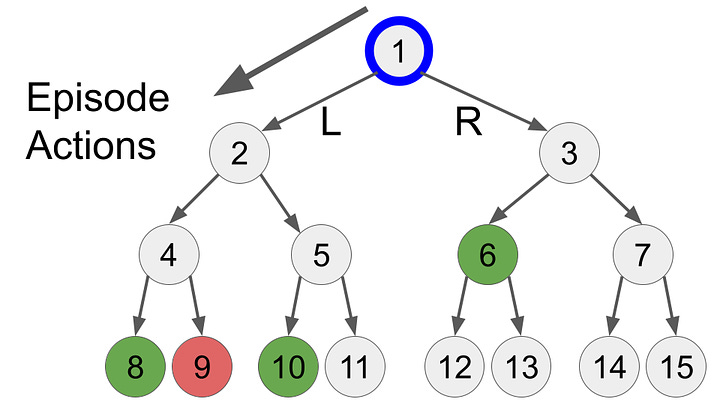
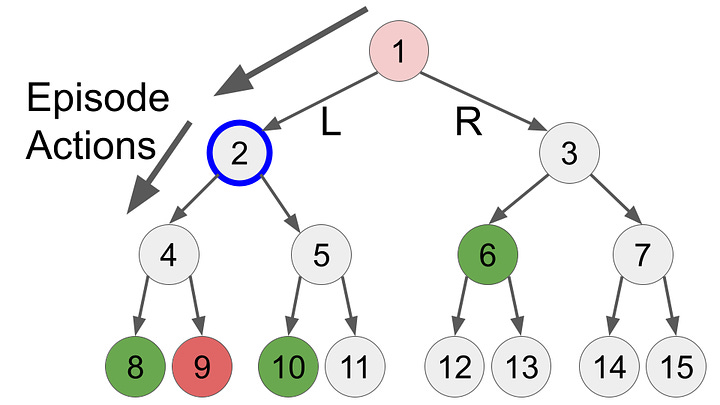
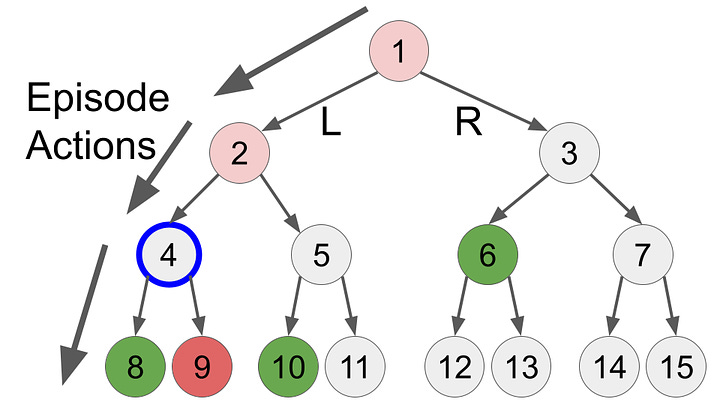
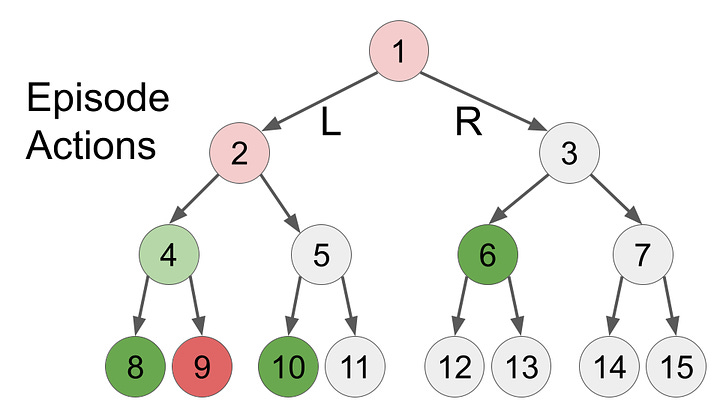
By the end of this first episode, the AI has updated that state 1 and 2 are slightly negative⁵, because they didn’t get reward in those states, but it learned that state 4 is good because it got a positive reward. In the next run, the AI would start with the action R because in the first run L was a bad action. But if the AI took the LLL path enough times, the positive reward would eventually propagate to the origin node and the AI would learn that LLL would give it a reward.

Answering the Block 2 Question

Okay, we’re ready to answer the Block 2 Question! Here’s why the AI (sometimes) learns the 11-step pattern and usually sticks with it (conditional on learning it originally).

1. The AI randomly stumbles around until it finds a viable strategy. In isolation, if the AI does an N-step plan repeatedly, after doing that plan N times the reward signal will propagate to the starting state, and the AI will “realize” that there’s a viable strategy with positive reward from start to finish. So in some sense it’s a race between the AI doing a 10-step plan 10 times vs doing an 11-step plan 11 times, and whichever one happens first will be locked in. The reality is more complicated than this because some steps are shared between plans, and the AI’s stumbling may contribute to learning one plan but not the other.

2. If the AI finds the 11-step plan before a 10-step plan, it will run the 11-step plan over and over to ingrain it as having positive reward. The 10-step plan is left partially-discovered, with several steps having negative reward.

3. In order to escape from the 11-step plan, the AI would have to make a different decision in a step like this:

   

   According to its Q-table, the AI has learned that breaking block 2 leads to high reward. But sometimes the AI acts randomly choosing up, left, right, or down at random:

   1. If it randomly moves up, it breaks block 2, which it was going to do anyway. No new learning.

   2. If it randomly moves left or right, that’s suboptimal (it can execute a 12-step plan at best) and it will learns that’s bad.

   3. If it randomly moves down it breaks block 14, and it has a chance to find the 10-step plan! But there’s a problem: the AI has almost no experience in situations where blocks 7 and 14 are gone but block 2 is still there, and which is critical because of our choice of architecture. This is a scary wilderness, and the AI doesn’t know how to act! To complete the rest of a 10-step plan the AI needs to then make 4 more perfect moves, which it’s unlikely to do. But if the AI instead randomly breaks block 2, it’s back in familiar (high-reward) territory! So the AI will learn that if it randomly breaks block 14 instead of 2, the correct thing to do is to “get back on track” by destroying block 2, rather than stumble around the wilderness of [block 2 but not 7 or 14].

So there’s the key insight: to learn the correct strategy, the AI needs to take the right random action not just once, but 5 times in a row, which greatly reduces the chance it will happen! Since the AI acts randomly with probably 0.1/ln(i+2) in episode i, the odds odds of the correct action is 0.1/(4*ln(i+2)), and the odds of all 5 correct actions happening in a row is is (0.1/(4*ln(i+2)))^5 which is tiny! So the AI could go a very long time without ever finding a 10-step plan.

Let’s wrap up with some math. Since (0.1/(4*ln(i+2)))^5>epsilon/i for a small epsilon and sufficiently large i, and since \sum_i (epsilon/i) diverges, the AI will eventually try the 10-step plan completely at random, and therefore with probability 1 will eventually settle into a 10-step plan. That should be a small relief, although the amount of time in that “eventually” is probably longer than the lifetime of the universe!

1. States encode the following info: Link’s position, whether Link picked up the crystal or not, whether the heart has spawned, which blocks have been destroyed (including the shopkeeper…), and whether Link has the enhanced capabilities.

2. In a normal session block 6 can’t be destroyed unless one of blocks 10-12 have been destroyed, so the second state pictured is impossible to reach.

3. I’ve heard the heuristic that if you want to execute N step plans, gamma should be at least 1-1/N. Our plans are 10-15 steps long, meaning gamma should be at least .9 or .93.

4. Using a smaller alpha lets you average reward across many episodes, which is especially important if there is a lot of randomness in your environment which you need to account for. In our case, the only randomness is the 50% chance Link has to kill the shopkeeper if Link doesn’t have enhanced capabilities. If we set alpha all the way to 1, the AI would learn faster, but for killing the shopkeeper in particular Link would oscillate between thinking it’s terrible (if he failed in the previous attempt and got punished) and thinking there’s no issue (if he succeeded).

5. I’m conflating whether the state itself is negative vs the action taken from that state. The values of the Q-table describe state-action pairs, although the learning algorithm also uses Q_max(S) which describes the maximum reward expected from a state.